Abstract
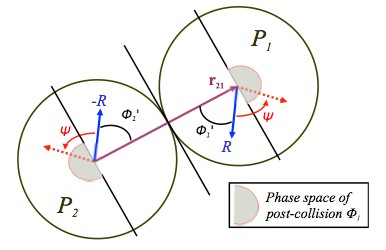
Consider a system of N identical hard spherical particles moving in a d-dimensional box and undergoing elastic, possibly multiparticle, collisions. We develop a new algorithm that recovers the precollision state from the post-collision state of the system, across a series of consecutive collisions, with essentially no memory overhead. The challenge in achieving reversibility for an n-particle collision (where, in general, n « N) arises from the presence of nd - d - 1 degrees of freedom (arbitrary angles) during each collision, as well as from the complex geometrical constraints placed on the colliding particles. To reverse the collisions in a traditional simulation setting, all of the particular realizations of these degrees of freedom (angles) during the forward simulation must be tracked. This requires memory proportional to the number of collisions, which grows very fast with N and d, thereby severely limiting the de facto applicability of the scheme. This limitation is addressed here by first performing a pseudorandomization of angles, which ensures determinism in the reverse path for any values of n and d. To address the more difficult problem of geometrical and dynamic constraints, a new approach is developed which correctly samples the constrained phase space. Upon combining the pseudorandomization with correct phase space sampling, perfect reversibility of collisions is achieved, as illustrated for n <= 3, d = 2, and n = 2, d = 3. This result enables, for the first time, reversible simulations of elastic collisions with essentially zero memory accumulation. In principle, the approach presented here could be generalized to larger values of n. The reverse computation methodology presented here uncovers important issues of irreversibility in conventional models, and the difficulties encountered in arriving at a reversible model for one of the most basic and widely used physical system processes, namely, elastic collisions for hard spheres. Insights and solution methodologies, with regard to accurate…